오늘은 퍼셉트론의 개념에 대하여 알아보는 시간을 갖겠습니다.
퍼셉트론(perceptron)은 인공 신경망의 한 종류입니다. 퍼셉트론에 대하여 알기 이전에 인공신경망이 무엇인지 잠시 살펴보고 가겠습니다.
인공신경망은 우리 뇌에 있는 '뉴런 (Neuron)'의 구조를 본따서 만들었습니다.

뉴런은 전기자극으로 신호를 전달하는 역할을 수행합니다. 전기 자극이 특정 역치를 넘기게 되면 신호를 옆으로 전달하게 됩니다.
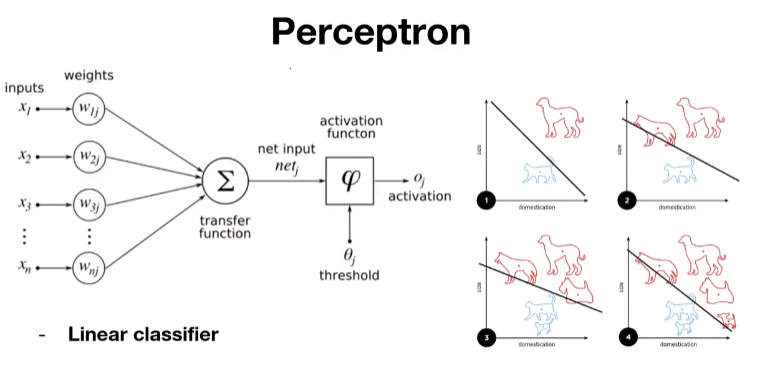
뉴런을 본따 만든 인공신경망 중 하나인 퍼셉트론은 전기자극에 해당하는 인풋값 x를 transfer function 을 통해서 weight 를 곱하고 그 가중치들의 합과 bias를 더해서 시그모이드 함수와 같은 activation function을 거쳐서 아웃풋이 됩니다.
초창기 퍼셉트론은 Linear classifier를 위해서 만들어진 모델입니다.
먼저 퍼셈트론은 AND 와 OR 를 해결하기 위한 방법으로 개발되었습니다.

AND 는 A 와 B 가 두개가 모두 만족했을 때 Y 라는 값을 가지게 되고 OR 는 A 혹은 B 중 하나만이라도 만족을 했을 때 Y 라는 값을 가지게 되는 매우 보편적인 개념입니다.
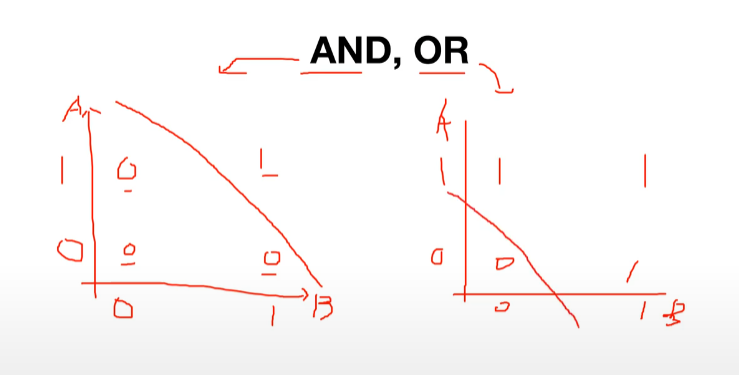
이렇게 그래프로 AND 와 OR를 그려보면 조금 더 직관적으로 확인 할 수 있습니다.
AND 와 OR를 이렇게 linear classifier 로 구분할 수 있는것을 확인하고 초기 컴퓨터 과학자들은 퍼셉트론을 활용해서 더 어려운 문제들을 해결해 줄 수 있겠구나 하고 생각했습니다.
이런 개념에서 우리 뇌의 뉴런과 연결하여 문제를 해결하다니 너무 놀랍습니다.

하지만 마빈 민스키라는 과학자가 XOR를 통하여 한개의 레이어 만으로 구성되어 있는 이 퍼셉트론 만으로는 대부분의 문제들을 해결할 수 없으며 학습하여 문제를 해결해 주기 위해서는 다중 레이어 즉 멀티 레이어가 필요하다는 것을 증명해 내면서 인공신경계는 암흑기로 빠져들었습니다.
위 그래프에서 보면 한 줄, 즉 linear classification 으로는 XOR의 문제를 해결할 수 없다는 것을 확인 할 수 있습니다.

그렇다면 이러한 퍼셉트론의 한계를 뛰어넘기 위해서 또 어떤 해결책을 생각해 보았을까요?
민스키 박사는 '멀티 레이어'를 활용한 퍼셉트론을 소개합니다.

'한 줄을 그어서 0 과 1을 나누지 못한다면 여러개의 레이어의 줄을 그어서 데이터를 나누어 주면 된다.'


이렇게 (W:5 b:-8), (W:-7, b=3), (W:-11, b:6)를 각각 시그모이드 함수에 대입하여 각각의 레이어를 거치게 된다면 우리는 XOR 값을 얻을 수 있다는 결론에 이르게 됩니다.
너무나도 천재적인 생각이지만 당시에는 누구도 이런 방법으로 w 와 b 값을 트레이닝 할 수 있는 방법을 고안하지 못해서 인공신경망 분야는 암흑기를 맞이합니다.
그리고 시간이 지나 이 문제를 해결 할 수 있는 방법으로 머신 러닝계의 핵심 방법이자 공부하면서 정말 많이 들으실 Back propagation 이라는 방법을 제안합니다.


입력값 X는 뉴럴 네트워크를 거쳐 결과값 Y를 갖게 되는데요, 아웃풋과 정답의 차이인 Cost (Loss)에 대해 뉴럴 네트워크의 weight 들에 대한 미분값을 계산을 하게 되고, 바로 뒤에 있는 weight 부터 loss 값을 최소화 시킬 수 있도록 뒤에서 부터 weight 를 업데이트 해 나가는 방식을 BackPropagation 이라고 합니다.

예시를 들어서 한번 개념을 더 구체화 시켜보겠습니다.
f = Wx + b 이라는 함수가 있고 Wx를 간단히 표현하기 위하여 g로 표현한다면 함수 f = g + b 로 표현할 수 있겠스니다.
위에 그림은 함수 f 를 그림으로 표현한 것입니다. W와 X 값은 곱해지고 거기에 b값이 더해지는 형태인데요, 여기서 알고 싶은것은 각각 w가 f의 결과값에, x가 f의 결과값에, b가 f의 결과값에 어떤 영향을 주는지를 알아낸다면 우리는 결과값을 가지고 w, x, b 를 추론 할 수 있을 것입니다.
즉 연쇄법칙 (chain rule) 을 사용한다는 말인데요 쉽게말해서 아~~~~ 무리 복잡한 함수라도 그 미분값을 구해주려면 각각의 요소의 미분값들을 곱해주면 된다는 법칙입니다.

그렇게 결과값에 미치는 영향 (미분값)을 뒤로 찾다보면 결국 이 전체적인 함수에서 인풋값이 어떤 영향을 주는지에 대해서 계산을 할 수 있게 되는겁니다.
그럼 위에서 보았던 XOR 문제를 Backpropagation을 코드로 확인해 보도록 하겠습니다.

코드를 실행 하기위해 torch 와 torch.nn 을 불러와 주고 device를 지정해 줍니다. 매번 값이 바뀌지 않도록 랜덤 시드 또한 설정을 해주겠습니다.

X와 Y에 각각 입력값을 정의해주겠습니다.

이제 XOR 문제를 해결하기 위한 다층 퍼셉트론 모델을 정의해주겠습니다.
입력층, 출력층 그리고 3개의 히든 레이어로 구성된 인공 신경망 (뉴럴 네트워크) 입니다.
그림으로 확인 한다면 다음과 같이 표현되겠습니다.


이제 비용 함수와 옵티마이져를 정의해 주겠습니다.
비용함수 (크로스 앤트로피 함수) 에서는 이진분류에서 사용하는 BCELoss 함수를 사용하고 옵티마니져로써는 SGD를 사용하도록 하겠습니다.
0 부터 10000 까지 10001번의 epoch 를 계산해주기 위해서 설정을 하고 각 에폭마다 backpropagation를 수행하게 됩니다.

epoch 이 거듭될수록 cost 값이 줄어드는 것을 확인 할 수 있습니다.
러닝이 잘 되었는지 확인을 하는 마무리 과정을 진행해보겠습니다.
