이전까지의 과제에서 우리는 활성함수 즉 activation function으로 시그모이드 함수를 활용했습니다.
시그모이드 함수는 0 혹은 1 이렇게 이진법으로 분류 할 때 사용하는 함수였죠?
하지만 우리가 사용한 시그모이드 함수에는 치명적인 단점이 존재합니다.

우리가 시그모이드 함수를 활용하여 Gradient를 구할 때 위에 파란색 부분에서는 정상적으로 Gradient를 구할 수 있지만 붉은 부분에서는 기울기가 너무 작아 0으로 수렴하기 때문에 Back propagation 에서 계속해서 앞단으로 gradient를 곱해 주면서 그 값이 너무 0과 가깝기 때문에 gradient가 끝까지 전파되지 못하고 중간에 소멸이 되는 경우가 생긴다는 겁니다. 이런 현상을 'Vanishing Gradient' 라고 부릅니다.


위 그림에서 보시는 바와 같이 forward 과정에서는 정상적으로 진행이 됐지만 back propagation 과정에서 vanishing gradient 현상으로 인해서 뒤로 갈수록 그라디언트가 전파되지 못하는 것을 확인할 수 있습니다.
이런 현상을 해결하기 위해서 나온 방법이 바로 ReLU 함수입니다.
그럼 ReLU 와 Sigmoid 함수가 어떻게 다른지 한번 살펴보도록 하겠습니다.
(렐루 그림 삽입)
보시는 것과 같이 파란색 부분에서는 그라디언트가 1이 되도록 하고 붉은색 부분에서는 그라디언트를 0으로 계산해주는 아주 간단한 함수입니다.
하지만 ReLU도 음수의 영역에서는 그라디언트가 0이 되기 때문에 사용에 주의를 해야겠습니다. 만약 음의 영역을 다루어야 한다면 조금 변형된 형태의 leaky_relu 함수를 활용합니다.
pytorch 에서 해당 함수들을 사용하는 코드는 아래와 같습니다.


이번에는 파이토치에서 제공하는 다양한 Optimizer에 대해 한번 알아보겠습니다.
파이토치.optim 패키지에서는 위와 같이 다양한 옵티마이져들을 제공하고 있습니다. 우리가 이전에 사용했던 SGD가 보이는게 괜히 반갑습니다.
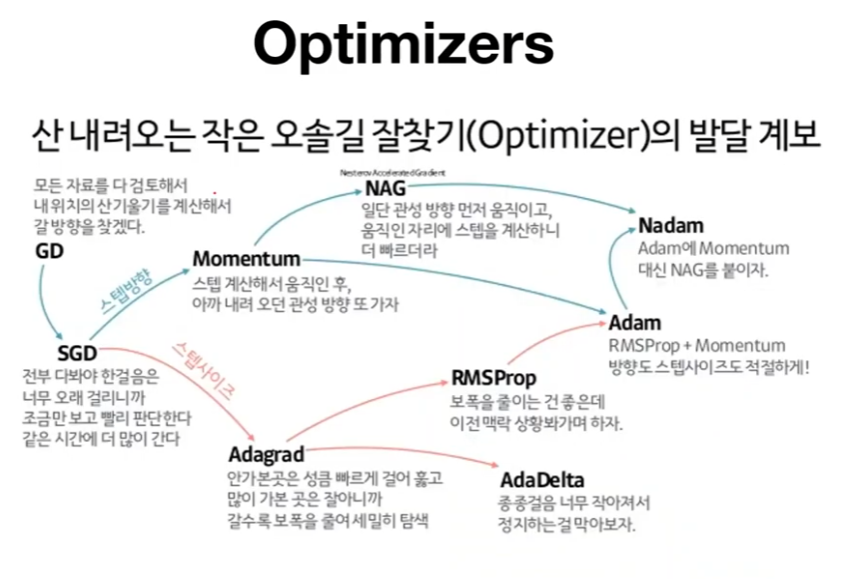
우리가 어느 상황에 어느 옵티마이져를 골라서 사용해야 할까 고민이라면 위에 옵티마이져 오솔길 그림을 확인하시면서 하나씩 따져가며 사용해 보고 결과를 확인해보는것도 좋은 방법일 것 같습니다.
그럼 멀티 레이어 구조에서 ReLU 를 활용한 코드와 싱글 레이어 구조를 비교해 보겠습니다.


Adam 옵티마이져를 쓴것을 확인 할 수 있습니다.

싱글 Fully connected layer 의 결과를 확인 하실 수 있습니다.

3개의 fully connected layer와 ReLU를 활용한 결과값입니다. 1개의 레이어에 비하여 훨씬 성능이 좋아지는 것을 확인하실 수 있습니다.